案例背景

Web 可视化页面展示应用中，有时需要显示场景的效果图，或是某一行政区划的透视视角图，并在上面添加有交互功能的点位标记，这些点位的位置坐标来源于真实场景的坐标系，这些坐标并不能直接使用在图上，因此需要借助一种映射计算方案，让前端可以直接将地理坐标转化为用于元素打点的绝对定位坐标。

本文通过多次实际项目应用，总结了 **平铺视角底图 **和 透视视角底图上打点的解决方案。

平铺视角-底图映射地理坐标系

在打点底图为平铺视角时，映射坐标相对比较简单。以给淮北市打点位置为例，首先打开附件中的【边界查询&坐标拾取工具】，如下图所示，分别为工具操作和视觉切图。

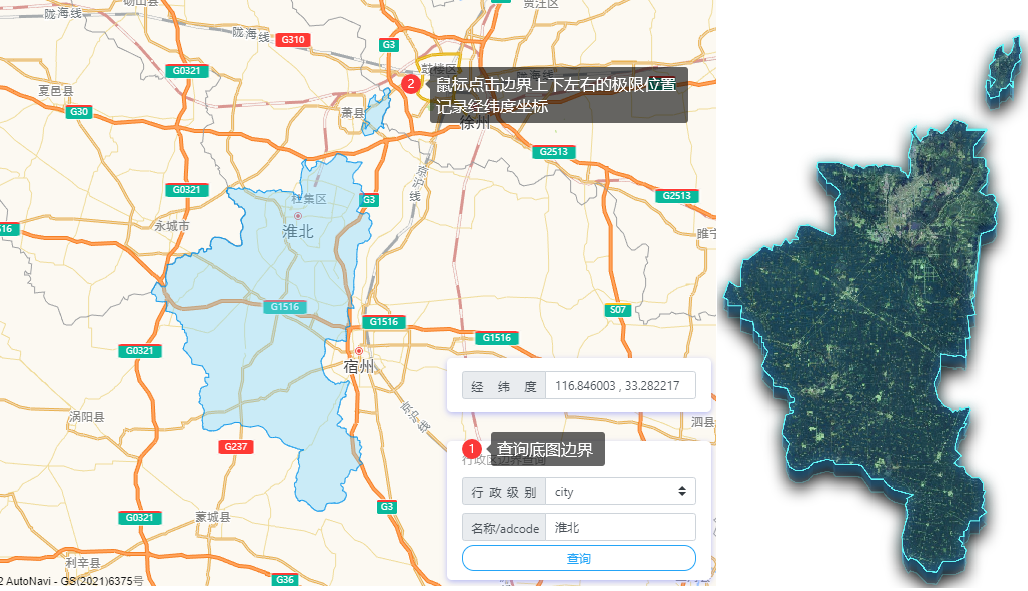
记录边界上下左右（也就是东南西北极点）的坐标，通过线性函数 getBottom 和 getLeft 计算每个点元素的绝对坐标即可。以下为示例：

<div
	v-for="(item, i) in data"
	:key="`icon${i}`"
	:style="{ bottom:getBottom(item), left:getLeft(item) }"
></div>

const boxline = [117.060818, 116.382723, 34.25501, 33.251408] // 东，西，北，南

methods: {
    getBottom (lonlat) {
      const value = (Number(lonlat.lat) - boxline[3]) / (boxline[2] - boxline[3]) * 100
      return value + '%'
    },
    getLeft (lonlat) {
      const value = (Number(lonlat.lon) - boxline[1]) / (boxline[0] - boxline[1]) * 100
      return value + '%'
    },
 }

透视视角-底图映射地理坐标系

在打点底图为透视视角时，情况就要更复杂一些，因为在屏幕的二维屏幕上，实际地理分布无法进行简单的线性映射了，因此需要一种透视映射算法，完成进一步的映射。下图展示的各种场景都可能会出现透视视角：

本章节将介绍这种情况下的应用实例和原创算法原理。

方案示例

以某科技园区鸟瞰图为例。

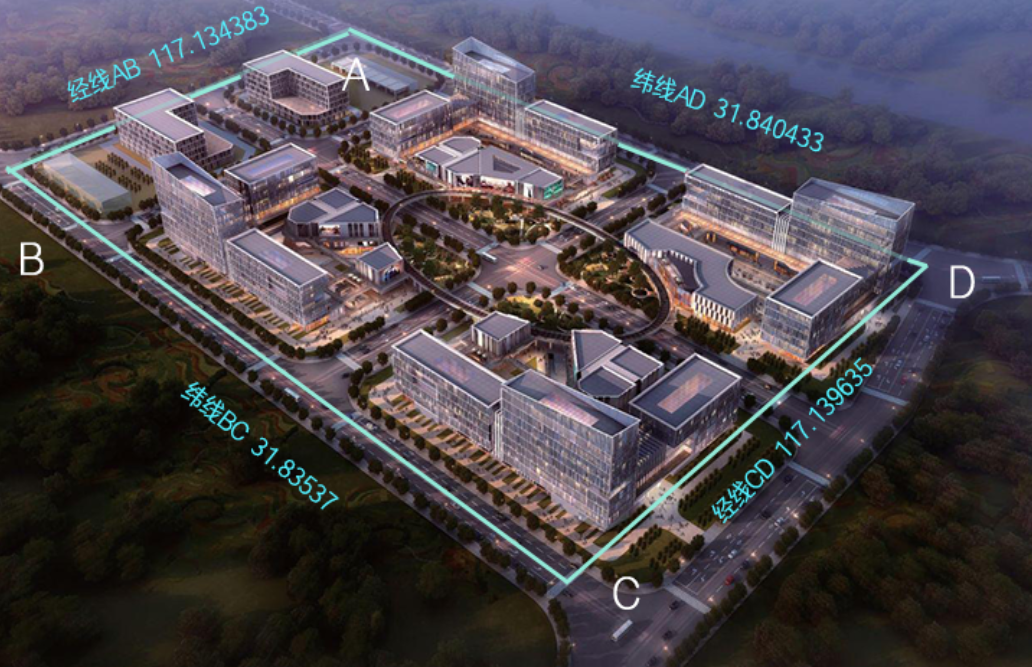
1. 查询该园区的电子地图，依据一些特征点（如路口、建筑物）在图中标记出 两条经线 和 两条纬线，形成一个四边形将园区囊括进去。这四条线在现实中应是两两平行的，但是在图中由于透视，所以并不平行。

   经纬度和特征点的确定同样可以使用附件中的【边界查询&坐标拾取工具】。

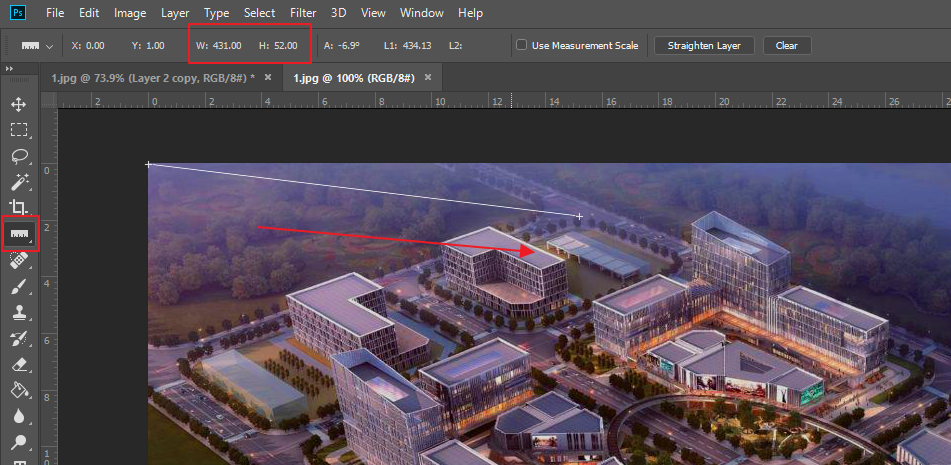
2. 测量四边形四个角点在图片上的坐标。以图片左上角为原点，推荐使用Photoshop中的标尺工具，可以看到下图测量得到得角点坐标为（431，52），代表这个点距离顶部52像素看，距离左侧431像素。测量完成4个点坐标后，即完成了映射参数的收集。

3. 在应用代码中，引入附件提供的映射算法文件perspectiveTrans.js，调用 getPerspectivePoi 函数，入参格式如下：

     import { getPerspectivePoi } from "./perspectiveTrans.js"
   
     const mark1 = [117.13963,31.8404] // 映射源地理坐标
     const calibrations = [
       [271, 30], // 起始角点
       117.134383, // 起始角点一侧的经线度数
       [8, 121], // 起始角点一侧的经线的另一侧角点
       31.83537, // 上面的点连接的纬线度数，下面依次排列
       [436, 436],
       117.139635, // 经线度数度数
       [708, 194],
       31.840433 // 纬线度数
     ]
    const poi = getPerspectivePoi(mark1, calibrations) // 映射后的图像坐标chenC

   其中参数 calibrations 为一个数组，数组成员依次为刚才在图片上测量到的角点和标线数据，对应案例图中，也就是 点A -> 线AB -> 点B -> 线BC -> 点C -> 线CD -> 点D -> 线DA。

4. 使用计算后的绝对定位坐标将点打在底图上，效果如下所示：

   

透视映射算法原理

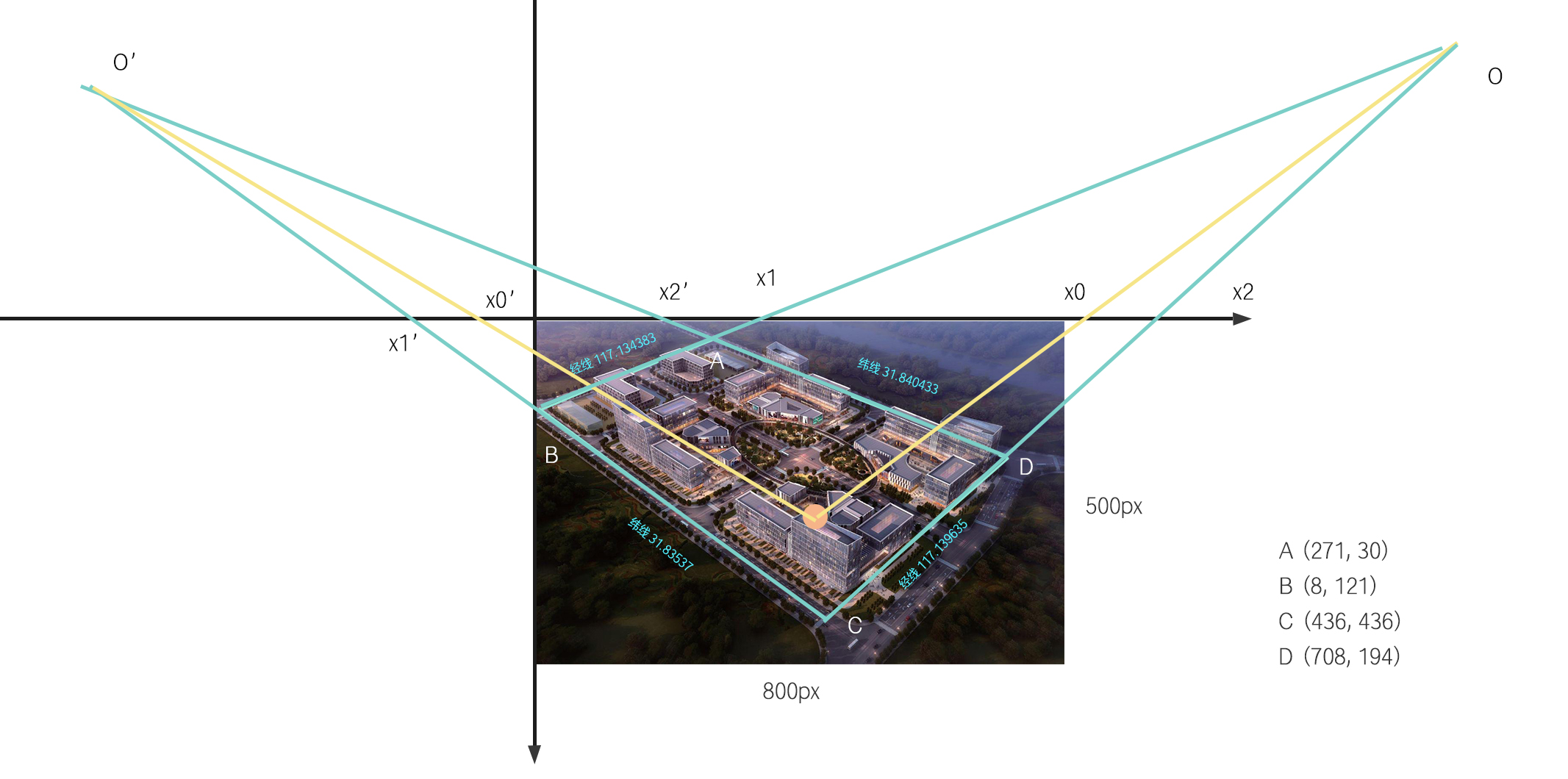
原本在现实中平行的经线和纬线，在有透视的情况下，则会在图中相交于一点，我们称之为“消失点”，如下图所示，点 O 和 O‘ 为消失点。根据测量所得的参数，可以计算：

1. 由 A、B、C、D 四点坐标，求四边形四条边在直角坐标系中的直线方程。

2. 由四条线的直线方程，求四条直线与 x 轴或 y 轴相交点的坐标。算法中会根据线的斜率判断计算x轴还是y轴，以防止线过于平行x轴或y轴，造成误差。图中选取的都是与x轴的交点，为 x1、x2、x1'、x2'。

3. 由四条线的直线方程，求消失点 O 和 O‘ 坐标值。

4. 设映射源标点与消失点的连线为图中黄线，黄线与x轴相交于x0、x0'。映射源坐标为(M, N)，标线经度为 m，m'，标线纬度为 n，n'，则有:

   (M - m) / (m' - m) = (x0 - x1) / (x2 - x1)，(N - n) / (n' - n) = (x0' - x1') / (x2' - x1')。由此求得 x0 和 x0‘ 坐标值。

5. 由 O 和 O‘ 坐标值，x0 和 x0‘ 坐标值，求得两条黄线的直线方程，两条黄线再求交点即为映射目标的坐标。

在附件 perspectiveTrans.js 中，将这个算法进行实现，代码如下：

/*
 * 入参，映射的经纬坐标 mark : [经度， 纬度]
 * 入参，图片的透视标定参数 calibrations，详见文档
 */

export const getPerspectivePoi = (mark, calibrations) => {
    const lon1 = calcLine(calibrations[0], calibrations[2]) // 经线1方程
    const lon2 = calcLine(calibrations[4], calibrations[6]) // 经线2方程
    const lat1 = calcLine(calibrations[2], calibrations[4]) // 纬线1方程
    const lat2 = calcLine(calibrations[0], calibrations[6]) // 纬线2方程
    const lonCrs = calcCross(lon1, lon2) // 经线方向上的消失点
    const latCrs = calcCross(lat1, lat2) // 纬线方向上的消失点

    if (lon1.k > -1 && lon1.k < 1) {
        const lonY = lon1.b + (mark[0] - calibrations[1]) / (calibrations[5] - calibrations[1]) * (lon2.b - lon1.b)
        var lonCrsToMark = calcLine(lonCrs, [0, lonY]) // 经线方向上的标点到消失点连线方程
    } else {
        const lonX = -lon1.b / lon1.k + (mark[0] - calibrations[1]) / (calibrations[5] - calibrations[1]) * (lon1.b / lon1.k - lon2.b / lon2.k)
        var lonCrsToMark = calcLine(lonCrs, [lonX, 0]) // 经线方向上的标点到消失点连线方程
    }
    
    if (lat1.k > -1 && lat1.k < 1) {
        const latY = lat1.b + (mark[1] - calibrations[3]) / (calibrations[7] - calibrations[3]) * (lat2.b - lat1.b)
        var latCrsToMark = calcLine(latCrs, [0, latY]) // 纬线方向上的标点到消失点连线方程
    } else {
        const latX = -lat1.b / lat1.k + (mark[0] - calibrations[3]) / (calibrations[7] - calibrations[3]) * (lat1.b / lat1.k - lat2.b / lat2.k)
        var lonCrsToMark = calcLine(lonCrs, [latX, 0]) // 经线方向上的标点到消失点连线方程
    }
    
    return calcCross(lonCrsToMark, latCrsToMark)
}

function calcLine(poi1, poi2) { // 求直线方程斜率和截距
    const x1 = poi1[0]
    const y1 = poi1[1]
    const x2 = poi2[0]
    const y2 = poi2[1]
    const k = (y2 - y1) / (x2 - x1) // 斜率
    const b = y1 - x1 * (y2 - y1) / (x2 - x1) // 截距
    return {k, b}
}

function calcCross(line1, line2) { // 求两直线交点
    const x = (line2.b - line1.b) / (line1.k - line2.k)
    const y = line1.k * x + line1.b
    return [x, y]
}